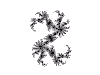Die Juliamenge zu einer komplexen Zahl z ist die Menge aller komplexen Zahlen c, für die die Folge (z_n) rekursiv definiert durch

betragsmäßg beschränkt ist. Benannt wurden sie nach dem französischen Mathematiker Gaston Julia.
Es lohnt sich, diese Definition mit der der Mandelbrotmenge zu vergleichen, damit man die Unterschiede nicht übersieht! Während es nur eine Mandelbrotmenge gibt, gibt es unendlich viele Juliamengen denn für jede komplexe Zahl lässt sich eine eigene Juliamenge berechnen.
Die Juliamenge zu einer komplexen Zahl z ist genau dann nicht-leer, wenn z in der Mandelbrotmenge ist, und genau dann ist das Julia-Fraktal zusammenhängend. (Daraus ergibt sich eine Charakterisierung der Mandelbrotmenge als Menge aller komplexen Zahlen z, deren Juliamengen nicht-leer sind!) Das Julia-Fraktal zu einer Juliamenge ist ein Bild, dass - ähnlich wie bei der Färbung der Mandelbrotmenge - veranschaulicht, wie schnell die oben definierte Folge für eine komplexe Zahl c betragsmäßig wächst. Es ergibt sich also auch ein schönes Julia-Fraktal, wenn die entsprechende Juliamenge leer ist.
Es gibt noch einen Zusammenhang zwischen Juliamengen und der Mandelbrotmenge: Das Julia-Fraktal zu einer komplexen Zahl z ähnelt stets einem entsprechenden Ausschnitt des Mandelbrot-Fraktals um diese Zahl z herum.